Visceral

Unit V

Image Transforms

Orthogonal Transform

// Ortho transform
A⁻¹ = Aᵀ

Unitary Transform

// Unitary transform
A⁻¹ = A*ᵀ = Conjugate(Aᵀ)

Properties of Image Transforms

// Symmetric
A == Aᵀ

// Orthogonal
A x A⁻¹ == A x Aᵀ == I

// Unitary
A x A⁻¹ == A x A*ᵀ == I

// Hermitian
A x A⁻¹ == A x A*ᵀ == A

// Interchange: if both A & B are symmetric, real, and orthogonal, then
A = P x B x Q       ===     B = P x A x Q

Hadamard Transform

  • It is a symmetric, non-sinusoidal function
// H (2x2)
H = (1 / sqrt(2)) |  1   1  |
                  |  1  -1  |

// H (4x4)
H = (1 / sqrt(4)) |  H   H  |
                  |  H  -H  |

  = (1 / sqrt(4)) |  1   1   1   1  |
                  |  1  -1   1  -1  |
                  |  1   1  -1  -1  |
                  |  1  -1  -1   1  |

// Similarly, H(8x8)
H = |  H   H  |
    |  H  -H  |

// One dimensional Haramard transform
F = H x f(x)

// Two dimensional Haramard transform
F = H x f(x, y) x Hᵀ        // which can be simplified to
F = H x f(x, y) x H
  • Sequencing is the number of sign changes in each row. N x 1

Haar Transform

  • Low computing requirement.
  • Great for image processing and pattern recognition.
  • Haar transforms are efficient for 2D image processing because of their wavelet-like structure.
  • Real and orthogonal.
  • Separable and symmetric.
  • Sequentially ordered.
  • Poor image compression.

Procedure to Generate Kernel of Haar

// Find the order N, and compute
n = log2(N)

// Determine p
p = [0, n - 1]

// Determine q
if(p == 0) { q = [0, 1] }
else{ 1 ≤ q ≤ 2^p }

// Determine k
k = 2^p + q - 1

// Apply the Haar function making necessary changes

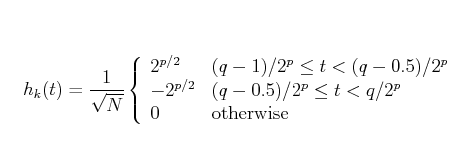
Haar Function

Resultant Haar Matrix

Haar Matrix

KL Transform

  • Unlike spatial and frequency based filters, KL transform works on statistical properties.
  • Mean, variance, standard deviation.
// Transform equation
Y = A (X - mean)

/* Y > output
 * A > KL transform matrix
 * X > object vector (x, y)
 * mean > Mean(X) */
  • Object vector X is formed by (x, y) location of 1s in the image.
  • Origin of axis is oriented at bottom left.

Procedure

  1. Calculate Mean(X)
  2. Calculate covariance matrix
Ci = (Xi - Mean(X)) x (xi - Mean(X))ᵀ   // 2x2 matrix
  1. Calculate Mean(C)
  2. Find the Eigen vectors and Eigen values
| C | = | C11 - λ       C12 | = 0
        | C21       C22 - λ |
  1. Form quadratic equation and solve for λ to find λ1 and λ2.

IMPORTANT

Number/assign λ1, λ2, λn such that their magnitudes are in decreasing order

| λ1 | > | λ2 | > ... > | λn |
  1. Solve for Eigen equation to get Eigen vectors
// Vector corresponding to λ1
| C11 - λ1       C12 | * | x_λ1 | = 0
| C21       C22 - λ1 |   | y_λ1 |

// Vector corresponding to λ2
| C11 - λ2       C12 | * | x_λ2 | = 0
| C21       C22 - λ2 |   | y_λ2 |
  1. Generate KL transform matrix A
A = | x_λ1    x_λ2    ...   x_λn |
    | y_λ1    y_λ2    ...   y_λ1 |
  1. Plug all the values in the KL transform equation

Solved Example Sample Problem

Skipped Topics

  • Two dimensional discrete fourier transform
  • Discrete cosine transform
  • Discrete sine transform